

We see real differences in acidity between substances when the of one is 100 or 1000 (or more!) times greater than the of the other.Ĭalculating PH allows us to measure acidity on a log scale of pH=14 to pH=0. However, a 1M difference in isn’t really meaningful. In chemistry, acidity can be measured on a linear scale from = 0.00000000000001M to = 1M. Modern computers have made those skills obsolete, but common logarithms still appear in problems like pH calculations where the underlying scale changes according to powers of 10. Mastery of logarithms was essential for scientists and engineers in the 19th and early 20th centuries because they could be used to simplify all kinds of complex calculations. Once you can do this, with a little practice, you can easily solve logarithms without needing a calculator.ĭo you have any logarithms you are unable to solve? Or do you have any questions for us? Please mention in the comments section below, and we will be happy to assist you.First a quick review of what logarithms are and why they are important on the MCAT: The common logarithm or “log” operator (sometimes seen as “log 10 “) is most useful when describing something that is measured on a very large scale. The other important part of solving a logarithm is understanding its exponential form. The most crucial part is to be well versed with squares, cubes, and roots of numbers. Solving a logarithm without a calculation is easier than it might seem. In the exponential form, this is equivalent to 2z = 321/2 This can be rewritten as log 2 (32)1/2 = z Let us convert it to exponential form (3/2)z = (27/8) This equation is not as difficult as it may seem. We know that 121 is 11 squared, and hence the square root of 121 is 11. To find z, first let us convert this to exponential form: 121z = 11 Here 64 needs to be converted to (1/4) raised to an exponent, which is the solution to the logarithm.
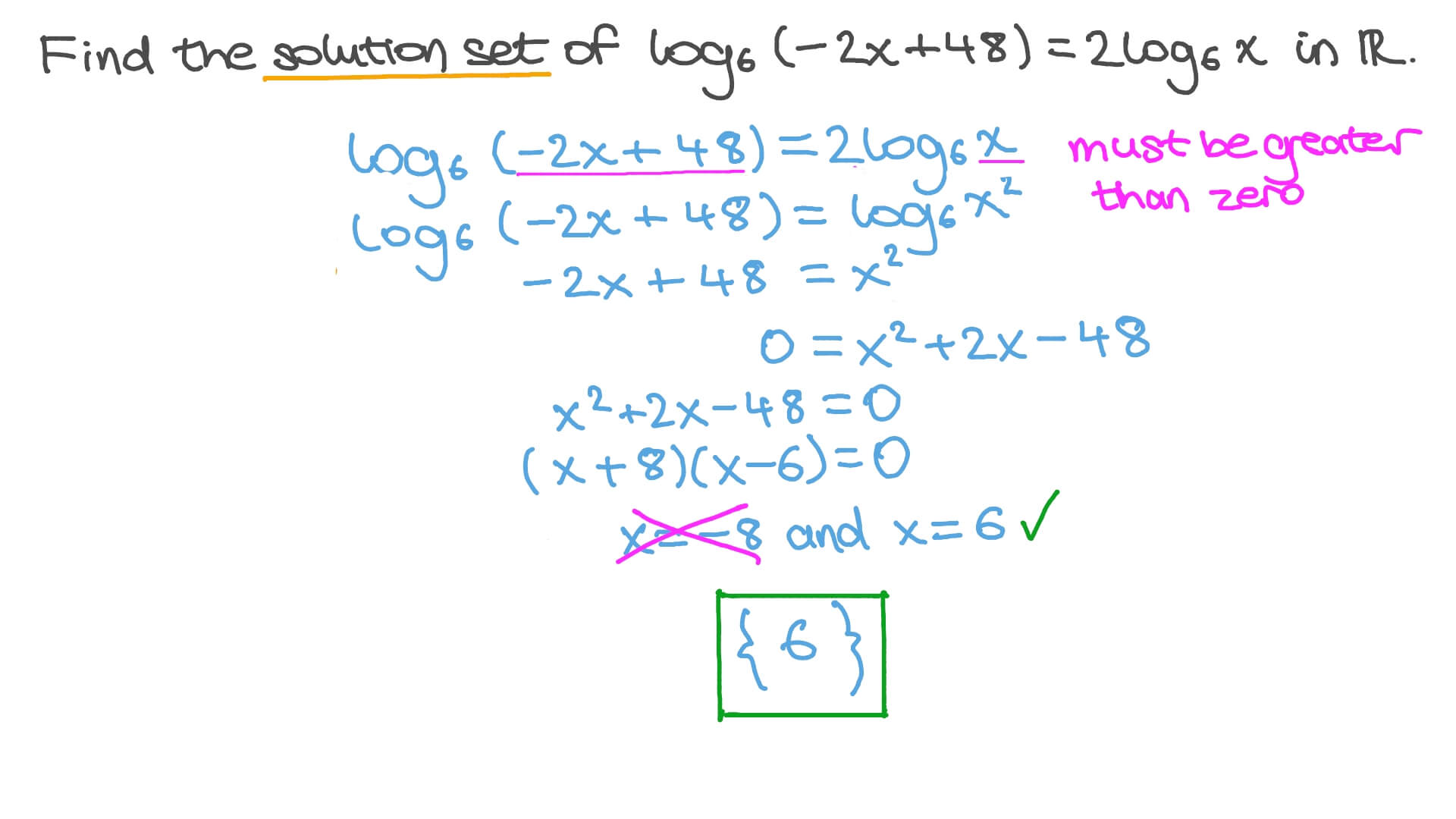
Now let us try to find z, by simplifying the equation This can be written in another form as: 4z = 1/64 Let us consider that log 4 (1/64) equals to z Some logarithms are more complicated but can still be solved without a calculator. In such cases, it is understood that the base value by default is 10. It is to be noted that in some instances you might notice that the base is not mentioned. One the base and the number in the parenthesis are identical, the exponent of the number is the solution to the logarithm. Let us try to replace the number in the parenthesis with the base raised to an exponent. Let us use an example to understand this further: log 5 (25)
Remembering and understanding this equivalency is the key to solving logarithmic problems. Here log x (y) is known as the logarithmic form, and xz = y is known as the exponential form. In other words, x needs to be raised to the power z to produce y. If xz = y, then ‘z’ is the answer to the log of y with base x, i.e., log x (y) = z The solution of any logarithm is the power or exponent to which the base must be raised to reach the number mentioned in the parenthesis.

We first need to understand square, cubes, and roots of a number.
#SOLVING LOGS HOW TO#
Now, let’s get to the main part: How to Solve a Log Without Using a Calculator? The number that needs to be raised is called the base. Defining a logarithm or logĪ logarithm is defined as the power or exponent to which a number must be raised to derive a certain number. To solve a logarithm without a calculator, let us first understand what a logarithm is. Logarithms are an integral part of the calculus.


 0 kommentar(er)
0 kommentar(er)
